MATEMATICAS

DESEMPEÑO: reconoce conceptos y herramientas preliminares del entorno Geogebra para desarrollar habilidades de orden superior

1. observa el vídeo expuesto por la docente.
2. De acuerdo a las instrucciones del vídeo realice en Geogebra:
A. triangulo y hexágono.
B. cuadrado y octágono.
3. Envié el archivo a la docente y publique una imagen del ejercicio.

SOLUCION
 2.
A.

B.

Desempeño 1:
                       Reconoce el entorno básico de geogebra a través de la interacción de sus herramientas para construir triángulos semejantes y rectángulos.

SISTEMAS DE ECUACIONES LINEALES:


En matemáticas y álgebra lineal, un sistema de ecuaciones lineales, también conocido como sistema lineal de ecuaciones o simplemente sistema lineal, es un conjunto de ecuaciones lineales (es decir, unsistema de ecuaciones en donde cada ecuación es de primer grado), definidas sobre un cuerpo o un anillo conmutativo. Un ejemplo de sistema lineal de ecuaciones sería el siguiente:



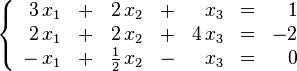
Método de sustitución

Supongamos que un sistema de ecuaciones se puede poner de la forma

[Unparseable or potentially dangerous latex formula. Error 3 ]

Entonces podemos despejar en la segunda ecuación y sustituirla en la primera, para obtener la ecuación: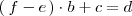



Lo que se busca es que esta ecuación dependa de menos incognitas que las de partida.




Aqui 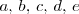y 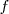son expresiones algebraicas de las incognitas del sistema.



 Ejemplo




Intentemos resolver



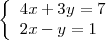
La primera ecuación se puede reescribir de la forma



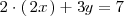
Por otra parte, de la segunda ecuación del sistema se deduce que



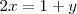
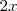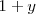Sustituyendo por en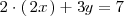



se tiene que



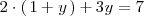
que es una ecuación con solo una incognita y cuya solución es .




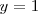Sustituyendo por uno en la primera ecuación del sistema de ecuaciones de partida obtenemos una ecuación de una sola incognita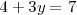





cuya solución es .



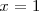Método Grafico
Consiste en construir la gráfica de cada una de las ecuaciones del sistema

El proceso de resolución de un sistema de ecuaciones mediante el método gráfico se resuelve en los siguientes pasos:

1.- Se despeja la incógnita (y )en ambas ecuaciones.

2.- Se construye para cada una de las dos ecuaciones de primer grado obteniendo la tabla de valores correspondientes.

3.- Se representan gráficamente ambas rectas en los ejes coordenados.

4.- En este último paso hay tres posibilidades:
a) Si ambas rectas se cortan, las coordenadas del punto de corte son los únicos valores de las incógnitas (x,y). "Sistema compatible determinado".

b) Si ambas rectas son coincidentes, el sistema tiene infinitas soluciones que son las respectivas coordenadas de todos los puntos de esa recta en la que coinciden ambas. "Sistema compatible indeterminado".

c) Si ambas rectas son paralelas, el sistema no tiene solución. "Sistema incompatible".

Ejemplos:


Entre Adriana y Carlos tienen 600 lempiras, pero Carlos tiene el doble de lempiras que Adriana. ¿Cuánto dinero tiene cada uno?.

Llamemos "x" al número de lempiras de Adriana y "y" al de Carlos. Vamos a expresar las condiciones del problema mediante ecuaciones:
Si los dos tienen 600 lempiras, esto nos proporciona la ecuación x + y = 600. Si Carlos tiene el doble de lempiras que Adriana, tendremos que y = 2x. Ambas ecuaciones juntas forman el siguiente sistema:

x + y = 600
2x - y = 0

Para resolver el sistema por el método gráfico despejamos la incógnita y en ambas ecuaciones y tendremos:

y = -x + 600
y = 2x

Vamos ahora, para poder representar ambas rectas, a calcular sus tablas de valores:

y=-x+600 y=2x
x y x y
200 400 100 200
600 0 200 400

Con estas tablas de valores para las dos rectas y eligiendo las escalas apropiadas en los ejes "X" y "Y", podemos ya representar gráficamente:






Descripción de la grafica

Si observamos la gráfica, vemos claramente que las dos rectas se cortan en el punto (200, 400), luego la solución del sistema es x = 200 e y = 400
La respuesta del problema planteado es que:
x=200 (Adriana)
y=400 (Carlos)